HP Challenge VA001 - Short Sweet Math Challenge 01 Trig IdentityHere you'll find in chronological order *all* Short & Sweet Math Challenges, Mini-Challenges and Semi-Regular Columns I've posted to the Museum of HP Calculators over the last decades. All of them are complete threads in PDF format, including my Original Post as well as all the usually very many replies posted by other MoHPC members and which you can download to read them at leisure with no internet connection required and thus no fear of eventual future unavailability.
The Challenges feature practically every HP calculator under the sun and then some, including all RPN and RPL models as well as the BASIC-programmable HP-71B, non-programmable models with a Solver and the HP Prime, plus occasionally calc models of other brands (TI, SHARP, CASIO, etc.) and even computers and assorted computer languages. My original solutions are given as well as most other people's, and extremely interesting topics and useful programming techniques and algorithms are described and developed at length, with enlightening comments galore.
This Category will also feature all new Challenges of any type I may write now and in the future. Stay tuned !
HP Challenge VA001 - Short Sweet Math Challenge 01 Trig Identity
12-page thread (18 posts), the very first one of my still-ongoing "Short Sweet Math Challenges" series, S&SMC for short, this one deals with an unexpected trig identity involving tangents.
HP Challenge VA002 - Short Sweet Math Challenge 02 Extreme Determinants
13-page thread (20 posts), this one deals with finding matrices whose determinants are extreme in a particular sense.
HP Challenge VA003 - Short Sweet Math Challenge 03 Powerful Numbers
20-page thread (19 posts), on finding all numbers less than some limit which have a certain interesting property.
HP Challenge VA004 - Short Sweet Math Challenge 04 Multiprecision Meanies
11-page thread (7 posts), three sub-tasks involving multiprecision and a final one which doesn't but it's nice nevertheless. Additionally, 12 useful Guidelines are given to help you write your own multi-purpose multiprecision library.
HP Challenge VA005 - Short Sweet Math Challenge 05 Rational Cardano
27-page thread (29 posts), in which you're asked to find cubic equations with integer coefficients that can be solved using Cardano's formula in a particularly pleasant way.
HP Challenge VA006 - Short Sweet Math Challenge 06 Everdivisible
6-page thread (8 posts), on finding a growing number with ever growing divisibility requirements.
HP Challenge VA007 - Short Sweet Math Challenge 06b Rooting for Cubics
28-page thread (40 posts). As you know, transcendental numbers cannot be the root of any polynomial equation with integer coefficients, whatever its degree. But this S&SMC asks you to try nevertheless.
HP Challenge VA008 - Short Sweet Math Challenge 07 Astounding Recursion
23-page thread (27 posts), a two-part S&SMC in which you're first asked to implement a given recursively-defined function, then you're asked to answer some questions about the function, using your implementation in order to help you discover its shocking nature.
HP Challenge VA009 - Short Sweet Math Challenge 08 Squares
29-page thread (34 posts), another two-parter, first asking for the unique square integer which has some specific property, then asking for all squares that fulfill a slightly relaxed variant.
HP Challenge VA010 - Short Sweet Math Challenge 09 Divisibility
42-page thread (43 posts), a three-pronged S&SMC which asks for integers that meet various divisibility requirements.
HP Challenge VA011 - Short Sweet Math Challenge 10 Counting Beans
12-page thread (15 posts), on finding the unique integer whose individual digits count certain digits present in the whole number, in a self-referential way (sort of ...)
HP Challenge VA012 - Short Sweet Math Challenge 11 Who Next
26-page thread (29 posts), on accepting a sequence of arbitrary numbers, then producing a sound prediction for the next element in the sequence.
HP Challenge VA013 - Short Sweet Math Challenge 12 Squaring Cubes
42-page thread (37 posts), on finding the smallest integer whose square is a certain sum of cubes.
HP Challenge VA014 - Short Sweet Math Challenge 13 Adding up to Infinity
34-page thread (44 posts), where you're given several infinite sums which you're asked to evaluate, then to identify the rational form of the results and, last but not least, to make a particular prediction about their nature.
HP Challenge VA015 - Short Sweet Math Challenge 14 Cooking Conjectures
56-page thread (36 posts), in which you're given three plausible conjectures (identified as "Well-done", "Medium" and "Rare" in order to whet your appetite) and then you're asked to write code to try and cook them up. Or not.
HP Challenge VA016 - Short Sweet Math Challenge 15 April 1st Spring Special
38-page thread (25 posts), first S&SMC of its kind ("April 1st Spring Special") in five Takes dealing with 4th-degree equations, tight cables surrounding the Earth, self-reproducing programs, uncanny recursive functions and more.
HP Challenge VA017 - Short Sweet Math Challenge 16 Thinking Square
38-page thread (31 posts), three-pronged S&SMC in which you're asked first to find certain self-reproducing squares 10-digit long, then 100-digit, then the works.
HP Challenge VA018 - Short Sweet Math Challenge 17 The Feast
31-page thread (33 posts), in which you're presented with a feast consisting of Appetizer, Main Course and Le Dessert, dealing with such things as the leftmost digits of powers of 2, a petit homage to the 41, and a conditionally convergent series which can be made to sum up to just about anything.
HP Challenge VA019 - Short Sweet Math Challenge 18 April 1st Spring Special
73-page thread (61 posts), a truly perplexing S&SMC in Eight Fits, all of them with highly unexpected and ... well, perplexing solutions, including lots of thinking-out-of-the-box involved. Fractional derivatives and squared factorials, anyone ?
HP Challenge VA020 - Short Sweet Math Challenge 19 Surprise
70-page thread (87 posts), a truly awesome 5-pronged, graded S&SMC, one of the very best, in which your solutions will get you Grades F, D, C, C+, B, B+, A or even A+, depending on your ingenuity and the quality of your code. For Grade A/A+ it even includes a kind comment by Mr. Thomas Schmelzer himself !
HP Challenge VA021 - Short Sweet Math Challenge 20 April 1st Spring Special
82-page thread (88 posts), includes a 3-pronged *training* part, then a full 5 cases sorted by difficulty (Simplest, Simpler, Simple, Less Simple, Least Simple), all of them truly jaw-dropping, with the last one's solution fully breaking into unexplored ground by producing new results never seen or published before.
HP Challenge VA022 - Short Sweet Math Challenge 21 Powers that be
22-page thread (28 posts), this is a new S&SMC inaugurating the "Second Season" of S&SMCs after an 8-year hiatus. It asks you to find and explore some very special constants that have an amazing, unexpected quasi-integer-powers property. High on math value as well as entertainment.
HP Challenge VA024 - Short Sweet Math Challenge 22 April 1st 2018 Spring Special
17-page thread (37 posts), a new "April 1st Spring Special" after a mere 10-year hiatus, structured around a Main Course and 4 Desserts, dealing with recognizing prime numbers, inaccurate inverse functions and much more.
HP Challenge VA026 - Short Sweet Math Challenge 23 May the 4th Be With You Special
33-page thread (50 posts), a "Star Wars"-themed S&SMC #23 "May the 4th Be With You" Special, featuring 6 Steps leading you from a newbie padawan to a deserved promotion to Jedi Knight should you manage to solve them all, which will require overcoming difficult limits and much thinking out of the box to succeed.
HP Challenge VA029 - Short Sweet Math Challenge 24 2019 Spring Special 5-tier
35-page thread (47 posts), a new "Spring Special" S&SMC#24, this time a 5-tier to give you all a chance to put to good use both your favorite HP calculator and your programming ingenuity. The tiers are, in approximate order of difficulty: Noob, Beginner, Intermediate, Advanced and Guru. Try them all and see what's your top one !
HP Challenge VA030 - Short Sweet Math Challenge 25 San Valentin Special - Weird Math
60-page thread (50 posts), a new "San Valentin's Special: Weird Math" S&SMC#25, featuring 6 Concoctions 6 dealing with weird, unexpected math results, including weird limits, weird infinite summations, weird integrals, weird graphs which are not what they seem to be, weird primes which are perfect in a very particular sense and last but not least, an alleged explanation on why some years are exceptionally catastrophic.
The various parts gathered much interest and a very lively discussion with plenty of code, graphics, solutions and comments being posted (included my original ones), as can be ascertained by the 60 pages in the thread.
Don't miss it, it's great fun and an opportunity to acquire new exciting knowledge !
HP Challenge VA101 - A Little HP-15C Challenge
7-page thread (15 posts), first simple challenge, on how to get a given value under severe restrictions.
HP Challenge VA102 - A little classical RPN challenge
14-page thread (27 posts), you're asked to perform some simple stackrobatics as economically as possible, which quickly evolves into a lively discussion and even generalized solutions.
HP Challenge VA103 - A little HP-71B challenge
2-page thread (4 posts), on recursively computing the factorial function, but with a very special quirk.
HP Challenge VA104 - Little HP-15C challenge for the weekend
5-page thread (11 posts), on computing a value with a stringent set of requirements, including doing it in a minimum number of steps.
HP Challenge VA105 - Two little RPN challenges (11C 15C).jpg)
3-page thread (6 posts), in which you're asked to compute two different values under heavy restrictions.
HP Challenge VA106 - Matrix Reloaded
13-page thread (18 posts), first part of a "Matrix Trilogy" of simple challenges, here you're asked to efficiently perform a certain matrix manipulation within specified conditions, again resulting in some very interesting solutions and lots of enlightening discussion.
HP Challenge VA107 - Matrix Convolutions
14-page thread (17 posts), second part of a "Matrix Trilogy" of simple challenges, here you're asked to generate a certain very useful matrix as fast and efficiently as possible. Again, very worthwhile discussion ensues.
HP Challenge VA108 - Matrix Trilogy
6-page thread (6 posts), third (and final) part of a "Matrix Trilogy" of simple challenges, a three-pronged concoction which asks you to find efficient solutions to all 3 different cases posited.
HP Challenge VA109 - Quiz Evaluating polynomials
12-page thread (11 posts), almost a sequel to the previous "Matrix Trilogy" of challenges, here you're asked to evaluate a number of polinomials (and ratios of polynomials) whose coefficients are given as elements in a matrix, for any given argument values, as fast and efficiently as possible. Very interesting proposed solutions and discussion thereof.
HP Challenge VA110 - HP-15C Arguably Useful Mini-Challenge
16-page thread (34 posts), on computing a well-known variation of the factorial function, with the main design goal for the solution to be as fast as possible (specially for large N) and, subject to that, to be as short as possible and/or to minimize resources used (registers, flags, etc) or in general to have some other desirable properties. Healthy amounts of discussion and many solutions offered.
HP Challenge VA111 - HP-15C Arguably Useful MC Sols Comments
10-page thread (10 posts), in which I give my original solutions to the "HP-15C Arguably Useful Mini-Challenge" whose details are given in the link immediately above this one, plus a number of relevant and interesting comments.
HP Challenge VA112 - Really really small HP-15C Mini-Challenge
9-page thread (20 posts), a really really small Mini-Challenge that asks for a simple but useful computation and which despite its simplicity attracted a number of nice solutions and many interesting comments.
HP Challenge VA113 - A little HP-15C Quiz for the Weekend
11-page thread (14 posts), in which you're asked 5 allegedly difficult questions about the HP-15C and its instruction set, in order to test your knowledge and ascertain whether you are eligible for "Guru" status or not.
HP Challenge VA114 - The Turtle (HP-71B) and the Hare (HP49G+)%20and%20the%20Hare%20(HP49Gp).jpg)
13-page thread (19 posts), the first part of a different kind of challenge where HP49G+ users (and other RPL models too) are asked to try their hand at performing & timing several common but complex tasks for comparison purposes with HP-71B's own timings.
The tasks include matrix operations, solving polynomial equations, Integrate & Solve combined, double integrals and triple integrals. Many people took the "challenge", which was successful enough that it engendered a second part and a "Results" thread to summarize it all. Very recommended.
HP Challenge VA115 - The 71B Turtle and 49Gp Hare Harder 2nd Half
24-page thread (28 posts), the second (and harder!) part of the "Turtle and Hare" challenge (link immediately above this one), featuring 5 additional, much harder tasks for RPL aficionados to try on their machines.
The tasks include complex-valued matrix operations, solving a definite integral of an implicit function, integrating a recursively-defined function, polynomial solver for roots of high multiplicity, and a probabilistic theoretical application involving multidimensional (4-nested!) integrals. This was again a huge success with many interesting, worthy discussions and of course tons of actual code and results.
HP Challenge VA116 - The 71B Turtle and 49G+ Hare Results
11-page thread (10 posts), in which I give my original timings for all 10 tasks proposed in the "Turtle and Hare" challenge (described above this one) using the HP-71B, with my Notes and comments by me and other interested people.
HP Challenge VA117 - Feigenbaum number
6-page thread (6 posts), in which I give two simple programs to compute the famous Feigenbaum's Constant (of Chaos Theory fame, fractals, etc.), for the HP-71B and the HP-15C respectively, with my Notes and comments. Not exactly a "challenge" but then again some people took the to it and tried to accomplish the same computation using their own HP models, with pretty satisfactory results.
HP Challenge VA118 - A New Small HP-15C Challenge
7-page thread (5 posts), in which you're asked to produce "professional"-looking code to perform 5 usual accounting-style tasks for a generic business, within given "client"'s requirements. Both my original solution and another correct one are included, again both fully commented, even at the step level.
HP Challenge VA119 - A Very Didactic Little Quiz
25-page thread (42 posts), which vividly illustrates the power of exponential growth. You're given two very different choices for making some money and you have to compute the outcome of each choice in order to see which one would you choose.
The two choices are really strikingly different and selecting the correct one can really go against commonsense. This challenge attracted a large number of posts with many solutions and interesting comments, many of them praising its didactic value.
HP Challenge VA120 - A Very Didactic Little Quiz Some Comments
7-page thread (11 posts), an extension to "Challenge VA119 - A Very Didactic Little Quiz" immediately above, plus extra code contributions and additional comments.
HP Challenge VA121 - HP-15C Mini-Challenge RSUM CSUM
7-page thread (11 posts), in which you're asked to efficienty implement fast versions of two useful matrix functions missing from the HP-15C's matrix function set. Complete with solutions and comments.
HP Challenge VA122 - New HP-15C mini-challenge
14-page thread (22 posts), in which you're asked to write code to produce a number of solutions to a particular Diophantine equation (i.e.: an equation in which all coefficients and results are assumed to be integers) resembling a generalized version of a very well-known quadratic equation. Lots of code, solutions and interesting comments included.
HP Challenge VA123 - Mini-Challenge Twiddling the bits
22-page thread (31 posts), a simple "challenge" in which you're asked to compute a number of bits of Euler's constant e (=2.71828...), perform some simple operations with them, and then watch the result in amazement. Despite being truly simple, this mini-challenge gathered a lot of attention, with many interesting results and side topics being extensively discussed.
HP Challenge VA124 - So your HP can INTEGRATE
26-page thread (24 posts), where you're asked to use your preferred calculator to try and find the value of 6 very difficult definite integrals. Lots of theory, results, and very interesting and didactic explanations on how to obtain them, plus tons of interesting comments by knowledgeable participants.
HP Challenge VA125 - HP-15C Mini-Challenge Speeding it up
50-page thread (81 posts), a fantastic Mini-challenge (even if I say so myself) where you're asked to wite code to sum a famous very slowly convergent series related to Pi and obtain 10 correct digits real fast.
I give two very short solutions, the fastest of which can do it in under a minute, and additionally this mini-challenge and the detailed explanation I give about its theoretical basis amazed and enthralled the participants (someone even says "I have to tell you, the recurrence of the pattern is downright spooky..."), resulting in one of the largest number of posts and comments (50 pages of them !) for any of my Challenges.
HP Challenge VA126 - HP-15C Mini-Challenge Impossibly Short
18-page thread (34 posts), in which you're asked to write what seems to be impossibly short code for finding a root of a generic cubic equation. Many interesting solutions, detailed explanations of their inner workings and underlying theory, as well as lots of comments and worthwhile discussion overall.
HP Challenge VA127 - HP-15C Mini-challenge
15-page thread (33 posts), in which you must write code to compute the sine function (of all things !) but under really really restricting conditions, and do it accurately, fast, and with a minimum of code. No mean feat, but many people attempted it and one even did *exactly* duplicate my original solution !. Lots of interesting approaches, unexpected theory, mesmerizing comments and useful discussion throughout.
HP Challenge VA128 - An HP-15C Mini-Quiz
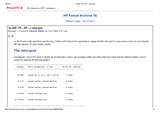
10-page thread (16 posts), in which you must try and duplicate a series of displayed values under various assumptions and using a given minimum number of steps. Many interesting and imaginative solutions, including my own for sure, with a good helping of comments.
HP Challenge VA129 - Valentine Day Mini-Challenges
81-page thread (98 posts), a very nice two-pronged Mini-Challenge on the topic of factorials, where as usual you're asked to produce results with extremely short amounts of code and further as fast and efficiently as possible.
This one really attracted the interest of the many participants (98 replies! 81 pages!) which posted a treasure trove of very clever solutions, full of interesting techniques and theory, plus lively discussion and worthwhile comments all over the place.
HP Challenge VA130 - Valentine Day MC A few modest insights Part 3
2-page thread (2 posts), an additional comment plus extra code to complement "Challenge VA129 - Valentine Day Mini-Challenges", described immediately above.
HP Challenge VA131 - Valentine Day MC A few modest insights Part 3
2-page thread (2 posts), some extra comments plus additional results for "Challenge VA129 - Valentine Day Mini-Challenges", described above.
HP Challenge VA132 - HP-15C Mini-Challenge Bits of Pi
51-page thread (68 posts), another incredible Mini-Challenge in which you're asked to produce in order the correct binary digits (at least 30 bits) of a value related to Pi, using a minimum amount of code.
Further, if you succeed you're given 3 additional related goals increasing the number of correct bits or under extra restrictions, always in a minimum of steps. This one also received widespread attention as demonstrated by the large number of posts and pages, including many excellent solutions, comments and very interesting underlying theory, plus tons of useful and entertaining discussion.
HP Challenge VA133 - HP42S Mini-Challenge Optimizing
56-page thread (37 posts), in which you're asked to try and find the one and only 12-digit square which meets a given requirement, chosing among three different goals: minimum size, maximum speed or a biased compromise between speed and size.
Again, this challenge attracted a large number of very good solutions, plus lots of comments and related discussion and of course my original solutions to all 3 goals are included.
HP Challenge VA134 - Valentine Day 2008 Mini-Challenge
41-page thread (38 posts), a three-pronged "Mini"-Challenge to commemorate my name's day, in which you're asked to write code to retrieve a set of numbers from a set of sums (5 sets to solve), to find the unique magic square which meets certain requirements, and last but not least, to find a set of numbers whose pairwise sums do have quite a nice property.
Once more this Mini-Challenge was well received and gathered quite a number of solutions (including my original ones, of course), comments and discussion. Matter of fact the challenge was originally posted with just one task to solve, then it was extended two times to turn things up a notch and keep the fun going on !
HP Challenge VA135 - HP-15C Mini-Challenge Magic squares
14-page thread (13 posts), where we visit magic squares again, and being given one you're asked to write code to derive another from it having a specified property, which of course you must do in a really minimum number of program steps.
A number of excellent solutions were given (including a most surprising one for the SHARP PC-1403 in BASIC, essentially a one-liner using no less than 5 calls to machine-code ROM routines to do all the work !) and also some pretty detailed, didactic and very well-formatted explanations of the theory involved.
HP Challenge VA136 - Pi Day Ramblings
24-page thread (31 posts), a challenge of sorts to commemorate Pi's Day, in which I give two very unusual ways to compute approximations to Pi and you're asked to find out how they work and provide your own favorite usual or unusual methods.
People took to it and actually posted a number of very interesting approaches in various programming languages, with lots of code, results, explanations and comments.
HP Challenge VA137 - HP-15C 11-11-11 Mini-Challenge
20-page thread (29 posts), a Mini-Challenge to commemorate the release of the HP-15C LE, in which you're asked to compute a numerical derivative for any given function and argument, subject to 5 very stringent requirements, including striving for full 10-digit accuracy and, of course, a minimum amount of code (else it wouldn't be much of a challenge).
I give my original solution in just 11 steps (which can be reduced to just 5 steps if relaxing some of the requirements) and people provided their own excellent ones and posted comprehensive details and comments.
HP Challenge VA138 - A Weekend Quickie
38-page thread (65 posts), a one-of-a-kind geometrical Mini-Challenge in which you're asked to compute some length given several others nearby. The correct solution also has a very interesting and unforeseen property.
It seems eople liked it and gave many fine solutions both numerical and exact (symbolic)`ones and further discussed and expanded the subject to a great extent. A very successful Mini-Challenge indeed.
HP Challenge VA139 - Birthday Commemorative Mini-Challenge
24-page thread (44 posts), a commemorative-style Mini-Challenge, actually a remake of a much older Mini-Challenge, in which you're asked to evaluate polynomials fast and accurately while subject to heavy restrictions. People gave many amazing solutions (using RPN, RPL, BASIC and even HP-12C's financial functions !!), and posted tons of interesting comments and discussion, as expected.
HP Challenge VA140 - Mini-challenge 3 lines of code
5-page thread (6 posts), in which you're asked to compute and display reasonably recognizable images of various fractal sets using the capabilities of your favorite HP (graphic or not) calc, including such well-known fractals as the Mandelbrot set, the Mandelbar (aka Tricorn), and the Burning Ship, doing it reasonably fast and using an absolute minimum of code.
In the very first post I included three 3-line programs for the HP-71B to compute and print said fractals for people to see exactly what was being asked, but sadly mine was the *only* code given, no one bothered to write and post a single line of code for any machine, or any relevant comments for that matter. A pity but there you are, you can't always succeed ... :)
HP Challenge VA141 - Introducing APRIL microchallenge
(20-page thread, 35 posts)
Let me introduce APRIL (Arithmetic Problem Recently Identified Locally), which is an arithmetic problem I recently identified locally while using some vintage HP calcs. The problem has been lurking unnoticed for 40+ years as of 2022.
To wit: there's a purely arithmetic operation that produces a result when executed in one series ("Spice": HP-33E/C, HP-34C ...) and a different one when executed in another series ("Nut" CPUs: HP-41, HP-10C, HP-15C ...). The term "arithmetic operation" does include √x but excludes all transcendental functions, statistics-related ones, yx, ->H.MS and ->HR.
The microchallenge: see if you can find such a faulty arithmetic operation. It will take some sleuthing to isolate the culprit but it can be done, and indeed several people successfully did it and posted correct solutions, apart from my original one, describing their sleuthing process in full detail. Really interesting stuff !
HP Challenge VA142 - Happy New Year 2024 and 2023s last teaser
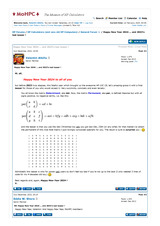
Happy New Year 2024 to all of you !
but before 2023 truly elapses, this fateful year which brought us the awesome HP-15C CE, let's amazing-grace it with a final teaser for those of you who would accept it.
Very succinctly, concisely and even tersely, you all know the matrix Determinant, aka det.
Now, the matrix Permanent, aka per, is defined likewise but with all products' signs positive, no negative terms, and the teaser is that you use the new Christmas toy calc you got last Dec, 25th (or any other, for that matter) to obtain the permanent of this nice little matrix I just lovingly concocted specially for you.
The result is sure to surprise you ! [...]
(15 pages, 31 messages, including solutions in 71B BASIC, RPL and SysRPL, plus comments and Greetings)
HP Challenge VA501 - SRC 001 Spiky Integral
33-page thread (45 posts), my first SRC, SRC#001, in which a very spiky integral featured in a math competition is introduced, together with my own simple RPN solution for the HP-15C which evaluates it as needed to help in answering the competition's problem. Then you're asked to produce your own code for your favorite calc and use it to get accurate numerical values to try and figure out the symbolic answer to the problem, as requested in the actual competition.
Many excellent solutions in a variety of languages, awesome extensions to much larger ranges complete with multiprecision evaluations, and lots of thorough theoretical explanations on how to get the symbolics right. Oh, and a little humour as well.
HP Challenge VA504 - SRC 002 Almost integers and other beasties
17-page thread (34 posts), my SRC#002, in which I present a number of interesting, short math expressions which unexpectedly evaluate to either almost integers or well-known constants, and you're asked to post your very own best ones with the proviso that you should've found them by yourself.
Many truly amazing new expressions, actual code, generalized results, interesting comments and all in all a worthwhile discussion. Oh, and a little humour as well. Again.
HP Challenge VA506 - SRC 003 New Year 2019 Special P01
17-page thread (20 posts), first page of my SRC#003, in which you're asked to create a certain 3x3 matrix and then compute its successive powers and the ratio of two particular elements in order to try and recognize the highly unexpected limit for this ratio.
As usual, lots of interesting results with many generalizations and full exposition of the relevant underlying theory, as well as code in various languages for diverse calc models. Extensions (to dimensions higher than 3x3, computing other limits and even obtaining roots of polynomial equations) are also discussed, including actual examples and results.
HP Challenge VA507 - SRC 003 New Year 2019 Special P02
4-page thread (7 additional posts), second page of "SRC 003 New Year 2019 Special", description and link immediately above this one.
HP Challenge VA508 - SRC 004 Fun with Sexagesimal Trigs
12-page thread (19 posts), in which you're asked to try and accurately evaluate 5 truly amazing trig expressions, in sexagesimal degrees no less, and should you succeed to then go on and identify the highly unexpected numeric results.
Not only did people succeed in evaluating the expressions and identifying the results, as asked to do, but additionally they posted many excellent symbolic proofs of each evaluation, even several different ones for each expression, with various degrees of simplicity (pun intended!).
HP Challenge VA509 - SRC 005 April 1st Mean Minichallenge
20-page thread (28 posts), my SRC#005, in which the symbolic formulas to evaluate the Harmonic, Geometric, Arithmetic and Quadratic Means are shown, complete with numerical results for a given sample set, then you're asked to write code to compute the numeric values of four other Means, and further to find out which particular Mean evaluates to a given result.
Seems simple but not so, though as usual interested people posted lots of code and results for various calcs (even for the HP39gII, with images), theoretical considerations, many worthwhile comments and even some quite amusing rants and interesting bits of history. Last but not least, an excellent pic of 12 awesome HP calcs was posted too, all of them duly identified. What more could you ask for !
HP Challenge VA511 - SRC 006 Pi Day 2020 Special
15-page thread (21 posts), in which a fast new method to compute Pi to any number of digits (millions, trillions and more) is described, as well as revisiting a couple of exotic methods I posted before which are quite unexpected, very rarely seen (if at all) and certainly interesting from a purely academic point of view (though utterly impractical as they're statistic in nature and thus quite slow). A lively discussion ensues.
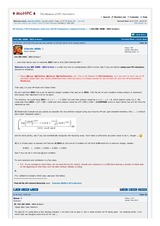
The new, fast method (which is self-correcting and converges cubically (the number of correct digits triples at each iteration) is compared with one of the best-known methods, the quartic one described in the paper "The Life of Pi: From Archimedes to Eniac and Beyond" by Jonathan M. Borwein et al. Actual code is given for Free42 (RPN, 7 steps) which computes 34 correct digits instantly, as well as an interactive session which produces 4, 11, 33, 100, 301 and 903 correct digits of Pi in just 6 extremely simple iterations.
HP Challenge VA512 - SRC 007 2020 April 1st Ramblings
13-page thread (17 posts), in which I present nine "Ramblings" for the readers to ponder and comment, ranging from solving highly unusual equations (even matricial ones) and systems of equations, to hyperbolics and Fibonacci numbers, finding exceptions to near identities, Star Trek's Cpt. Kirk having to solve a tricky scenario, plus assorted math curiosities.
As always, lively discussion ensues, all of them get solved by the participants and I give my own solutions and comments as well.
HP Challenge VA513 - SRC 008 2021 is here
19-page thread (41 posts), in which I give a warm welcome to New Year 2021 by proposing three interesting little problems featuring 2021 for the readers to solve, including an amazing definite integral which will surprise everyone and their uncle, plus two nice, easier problems.
Lots of code, exact results, theoretical explanations and assorted comments were posted by a number of MoHPC forum members, including my own original ones. Pretty interesting reading at any rate plus you may try and solve them on your own as well.
HP Challenge VA514 - SRC 008 2021 is here - Printable
18-page thread (41 posts), this is the Printable version of the above HP Challenge VA513, which I include here as well because source code included in CODE panels is hidden in the PDF version above but appears visible in this Printable version. On the other hand, mathematical formulas aren't presented graphically in this version but only as MathJax tags, while they're correctly presented in the PDF version above, so both versions are necessary for completeness.
Please refer to the above version for the challenge's description proper.
HP Challenge VA515 - SRC 009 Pi Day 2021 Special
28-page thread (38 posts) commemorating Pi Day 2021, including 6 new assorted appearances of Pi and other trivia, such as two very aesthetically pleasing integral equations (one of them somehow connecting Pi with Lambert's W function), a seemingly unexpected finite expression giving Pi as a function of e, an unexpected result for the summation of the volume of certain hyperspheres, ramblings on Kate Bush and Pi, The Simpsons and Pi, links to some unbelievable (literally !) "peer reviewed" papers on Pi and even a bilingual small joke (very small).
Lots of code, theoretical explanations, results, and plenty of interesting comments, including my extensive original ones. A very good way to have fun while learning some interesting facts in the process.
HP Challenge VA516 - SRC 010 Pi Day 2022 Special
This SRC is intended to once again commemorate this most famous of constants, Pi. After posting many threads over the years about Pi, it would seem difficult to find new, interesting appearances of it but actually that's not the case at all, Pi is inexhaustible and to prove the point I introduce here a new appearance, namely an unexpected infinite product for Pi, plus four exciting related questions.
19-page, 20-post thread featuring very interesting replies by forum members, and a lot of RPN and HP-71B code to sleuth the answers away. Also, a serious flaw in the internal code used in Free42 for large integer exponents was serendipitously unearthed.
HP Challenge VA517 - SRC 011 April 1st 2022 Bizarro Special
A commemorative SRC intended to once again put your brains and your HP calculators to work, this time featuring a challenge based on a bizarre topic which nevertheless has useful real-life applications. The challenge is introduced within a fictional story I concocted for the occasion based on DC 's character Bizarro #1 and the cube-shaped planet where the Bizarro people live.
In the end, you're asked to numerically evaluate a complex six-dimensional definite integral using an HP-10C, of all things.
22-page, 35-post thread, with many worthwhile contributions, lots of fun, graphics, pics, references, plus RPN & HP-71B code galore.
HP Challenge VA518 - SRC 012a Then and Now - Probability
This is a brand-new multi-part SRC #012 - Then an Now, where I'll convincingly demonstrate that some advanced vintage HP calcs which were great problem-solvers back THEN in the 80's (some 40 years ago !), are NOW still perfectly capable of solving recently-proposed non-trivial problems intended to be tackled using modern 2020-era personal computers, not ancient pocket calcs.
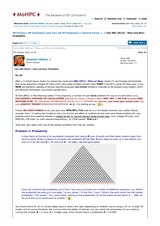
Problem 1: Probability
A man starts at the top of an equilateral triangular grid having R rows of points and then takes random steps from point to point. Write a program to compute the probability P that after S such steps he ends up in the bottom row, and run it for the case R = 30 rows and S = 60 steps, see the figure below [...]
61-page, 89-post thread, with solutions written in RPN, RPL, System RPL, HP-71B BASIC, SHARP PC-1403H BASIC and other languages.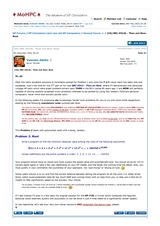 HP Challenge VA519 - SRC 012b Then and Now - Root
This is the 2nd part of my new SRC #012 - Then an Now arc.
Problem 2: Root
Write a program to find the minimum absolute value among the 10,000 roots of the following 10,000th-degree polynomial:
P(x) = 2 + 3 x + 5 x2 + 7 x3 + 11 x4 + 13 x5 + ... + 104743 x10,000
whose coefficients are the prime numbers in order: 2, 3, 5, 7, 11, 13, ... , 104743.
HP Challenge VA520 - SRC 012c Then and Now - Sum
This is the 3rd part of my new SRC #012 - Then an Now arc.
Problem 3: Sum
Write a sumptuous program to summarily sum this unassuming yet serious series:
where f(n) is defined thus: if n < 3 then f(n) = n else f(n) = n * f(d(n)), where d(n) = number of binary digits of n [...]
HP Challenge VA521 - SRC 012d Then and Now - Area
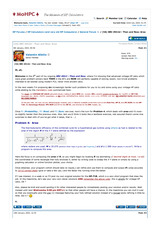
This is the 4th part of my new SRC #012 - Then an Now arc.
Problem 4: Area
The thermodynamic efficiency of the combined cycle for a hypothetical gas turbine using ethane as fuel is related to the area of the region R of the X-Y plane defined by the expression
where radians are used, M is 30.070 (ethane's Molar mass in g/mol) and d is 1.598 (Molar density in mol/dm3). Write a
program to compute this area [...]
HP Challenge VA522 - SRC 012e Then and Now - Roots
This is the 5th part of my new SRC #012 - Then an Now arc.
Problem 5: Roots
Write a program to compute and output the 7 largest positive real roots of R(x) (Riemann's Prime Counting function), in decreasing order.
You can use any equivalent form of R(x) that suits you best, be it the canonical definition or the one I used in my article and in the examples here, or any other you deem appropriate [...]
HP Challenge VA523 - SRC 012f Then and Now - Angle
This is the 6th and final part of my new SRC #012 - Then an Now arc.
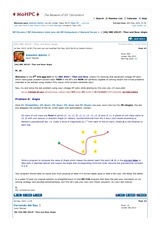
Problem 6: Angle
Six stars of unit mass are fixed at points (2, -1), (2, 0), (2, 1), (3, -1), (3, 0) and (3, 1). A planet of unit mass starts at (0, 0) with unit velocity in direction Angle (in radians, counterclockwise from the X axis,) and travels according to
Newton's gravitational law, [...]
Write a program to compute the value of Angle which makes the planet reach the point (4, 1) in the shortest time (a fake path is depicted above) and output the Angle and corresponding minimum time. Assume the gravitational constant G is 1 [...]
HP Challenge VA524 - SRC 013 Pi Day 2023 Special
This SRC #13 is intended to commemorate once more this most ubiquitous constant. After posting a number of threads over the years about Pi Day, such as these,
SRC #010 - Pi Day 2022 Special
SRC #009 - Pi Day 2021 Special
SRC #006 - Pi Day 2020 Special: A New Fast Way to Compute Pi
it would seem problematic to find new, intriguing appearances of the little critter but far from it, it's well-nigh inexhaustible and to prove the point let me introduce a couple' additional appearances for your enjoyment [...]
27-page, 33-post thread, with solutions written in RPL, System RPL, HP-71B BASIC and other languages for the main challenge plus assorted related extensions.
HP Challenge VA525 - SRC 014 HP-15C and clones Accurate NxN Determinants
(13-page, 11-post thread)
HP Challenge VA526 - SRC 015a - HP-15C and clones Big NxN Matrix Inverse Determinant
Welcome to this SRC #15 I created to commemorate the HP-15C Collector's Edition, which boasts enormously increased processing speed (up to 180x) and memory (up to 3x.)
However, there's a significant problem, namely that although the memory is vastly increased in most 15C clones (physical or virtual), allowing the dimensioning and use of matrices larger than 8x8, some very important advanced matrix operations (namely matrix inversion, system solving and determinant) can't be confidently performed using such large matrices (unreliable results, blocked calculator) due to firmware limitations.
My solution is to adopt an entirely new strategy which uses the built-in microcoded inversion instruction for speed, but making sure it never has to invert a matrix larger than 8x8 ! . Enter partitioned matrices [...]
(24-page, 18-post thread.)
HP Challenge VA527 - SRC 015b HP-15C and clones COMPLEX Matrix Inverse up to 8x8
Welcome to this second part of my thread SRC #015 - HP-15C & clones: Big NxN Matrix Inverse & Determinant, which I created to commemorate the availability of the HP-15C Collector's Edition.
The first part dealt with computing the NxN real matrix inverse and determinant for large values of N (2 ≤ N ≤ 16, subject to available memory, of course,) in particular for N exceeding the HP-15C's firmware limitation of 8x8 matrices. Additional posts to that thread further dealt with:
Real matrix inversion and determinant up to 13x13 (my OP)
Real linear systems up to 13x13,
Complex matrix inversion up to 6x6
Complex systems of equations up to 6x6,
Computing the absolute value of the determinant of a complex matrix up to 6x6.
However, in the particular case of complex matrix inversion we can do better than 6x6, as we'll see now [...]
(24-page, 19-post thread.)
HP Challenge VA529 - SRC 017 April 1st 2024 Spring Special
Once again April 1st is here and I want to celebrate both it and the new season with this Spring Special where I'm proposing a number of mini-challenges for you to tackle with your favorite vintage HP calc, plus interesting facts not widely known (if at all):
1. LOL the First: SquaresCOPYRIGHT NOTICE
These articles, programs, pictures, their descriptions and other materials created by me
are (c) Valentin Albillo, and can be used freely for non-profit purposes
as long as (1) the contents aren't modified in any way and (2) the copyright is acknowledged.
In plain words, you can download them and use them for non-profit purposes but do not include
them in any media and/or site for which you're asking money, do not tamper with their contents and
do not say or imply that you created them or that you don't know who created them, you must
always give due credit to me.